| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 파이썬라이브러리
- 머신러닝
- CSS
- 데이터베이스
- 자바
- SQL
- 중학1-1
- 파이썬
- 정보처리기사필기
- 코딩테스트
- 연습문제
- CNN
- html/css
- JSP/Servlet
- pandas
- 컴퓨터비전
- 데이터입출력구현
- 컴퓨터구조
- numpy/pandas
- 혼공머신
- 중학수학
- 정수와유리수
- 데이터분석
- 딥러닝
- 영어공부
- 자바 실습
- C++
- 정보처리기사실기
- 운영체제
- 텍스트마이닝
- Today
- Total
클라이언트/ 서버/ 엔지니어 "게임 개발자"를 향한 매일의 공부일지
이미지를 위한 인공 신경망 3 - 합성공 신경망을 사용한 이미지 분류 1 : 합성곱 신경망 만들기 본문
아침에 공부를 하다가 너무 졸려서 낮잠을 무려 4시간 반이나 자고 오후 늦게 일어나고 말았다. 가끔씩 이렇게 잠이 많이 필요한 날이 있다. 일어났을 때는 시간낭비를 굉장히 많이 한 것 같아 스스로에게 화가 나기도 했지만 다시 마음을 회복하며 공부의 자리에 앉아본다.
사실 아침에 학교 수업의 영상을 들었지만 생각했던 것만큼 의미 있는 수업이 아니라서 무척 실망스러웠던 것 같다. 그리고 차라리 수업을 듣지 말고 책 두 권으로 학습을 진행할까 고민했던 것 같다. 그럼에도 공부를 진행해야겠다고 생각했다.
난 강의보다는 책으로 훨씬 더 잘 이해를 하는 편이라는 걸 알게 되기도 했다. 소리는 금방 들으면 잊어버리고 무슨 말인지 이해가 잘 안 된다. 하지만 글자는 분명하고 여러 번 반복해서 읽을 수 있다는 장점이 있다. 강의를 진행하는 이유는 사람들은 대부분 책을 통해서 지식을 습득하는 것을 좋아하지 않기 때문인 것 같다. 그리고 현장에서 공부하지 않으면 하지 않는 사람들이 많은 이유이기도 하다.
어쨌듯 오늘은 최대한 많은 시간 공부를 해볼 것이다.
시작하기 전에
텐서플로를 사용하면 합성곱, 패딩, 풀링 크기를 직접 계산할 필요가 없다. 복잡한 계산은 케라스 API에 모두 위힘하고 사용자는 직관적으로 신경망을 설계할 수 있다. 하지만 합성곱 계산 방법을 잘 이해하면 합성곱 신경망 이면의 동작 원리를 터득할 수 있고 특히 다른 사람이 만든 신경망의 구조를 이해할 때 도움이 된다.
이번 절에서는 텐서플로 케라스 API를 사용해 만들었던 패션 MNIST 데이터를 합성곱 신경망으로 분류해 보겠다.
패션 MNIST 데이터 불러오기
먼저 케라스 AI를 사용해 패션 MNIST 데이터를 불러오고 적절히 전처리하겠다. 데이터 스케일을 0~255 사이에서 0~1 사이로 바꾸고 훈련 세트와 검증 세트로 나눈다.
여기에는 한 가지 작업이 다르다. 완전 연결 신경망에서는 입력 이미지를 밀집층에 연결하기 위해 일렬로 펼쳐야 한다. 이 작업을 위해 넘파이 reshape() 메서드를 사용하거나 Flatten 클래스를 사용했다. 합성곱 신경망은 2차원 이미지를 그대로 사용하기 때문에 일렬로 펼치지 않는다.
다만 앞장에서 언급했듯이 입력 이미지는 항상 깊이(채널) 차원이 있어야 한다. 흑백 이미지의 경우 채널 차원이 없는 2차원 배열이지만 Conv2D 층을 사용하기 위해 마지막에 이 채널 차원을 추가해야 한다.


이제 (420000, 28, 28) 크기인 train_input이 (48000, 28, 28, 1) 크기인 train_scaled가 되었다.
합성곱 신경망 만들기
전형적인 합성곱 신경망 구조는 합성곱 층으로 이미지에서 특징을 감지한 후 밀집층으로 클래스에 따른 분류 확률을 계산한다. 케라스의 Sequential 클래스를 사용해 순서대로 이 구조를 정의해 보겠다.
먼저 Seequential 클래스의 객체를 만들고 첫 번째 합성곱 층인 Conv2D를 추가한다. 이 클래스는 다른 층 클래스와 마찬가지로 keras.layers 패키지 아래에 있다. 여기서는 이전 장에서 보았던 모델의 add() 메서드를 사용해 층을 하나씩 차례로 추가하겠다.


이 합성곱 층은 32개의 필터를 사용한다. 커널의 크기는 (3, 3)이고 렐루 활성화 함수와 세임 패딩을 사용한다. 완전 연결 신경망에서처럼 케라스 신경망 모델의 첫 번째 층에서 입력의 차원을 지정해 주어야 한다.
그다음 풀링 층을 추가한다. 케라스는 최대 풀링과 평균 풀링을 kdras.layers 패키지 아래 MaxPooling2D와 AveragePooling2D 클래스로 제공한다. 쩐형적인 풀링 크기인 (2, 2) 풀링을 사용해 보겠다. Conv2D 클래스의 kernel_size처럼 가로세로 크기가 같으면 정수 하나로 지정할 수 있다.

패션 MNIST 이미지가 (28, 28) 크기에 세임 패딩을 적용했기 때문에 합성곱 층에서 출력된 특성 맵의 가로세로 크기는 입력과 동일하다. 그다음(2, 2) 풀링을 적용했으므로 특성 맵의 크기는 절반으로 줄어든다. 합성곱 층에서 32개의 필터를 사용했기 때문에 이 특성 맵의 깊이는 32가 된다. 따라서 최대 풀링을 통과한 특성 맵의 크기는 (14, 14, 32)가 될 것이다.
두 번째 합성곱-풀링 층을 추가해 보겠다. 첫 번째와 거의 동일하지만 필터의 개수를 64개로 늘린 점만 다르다.
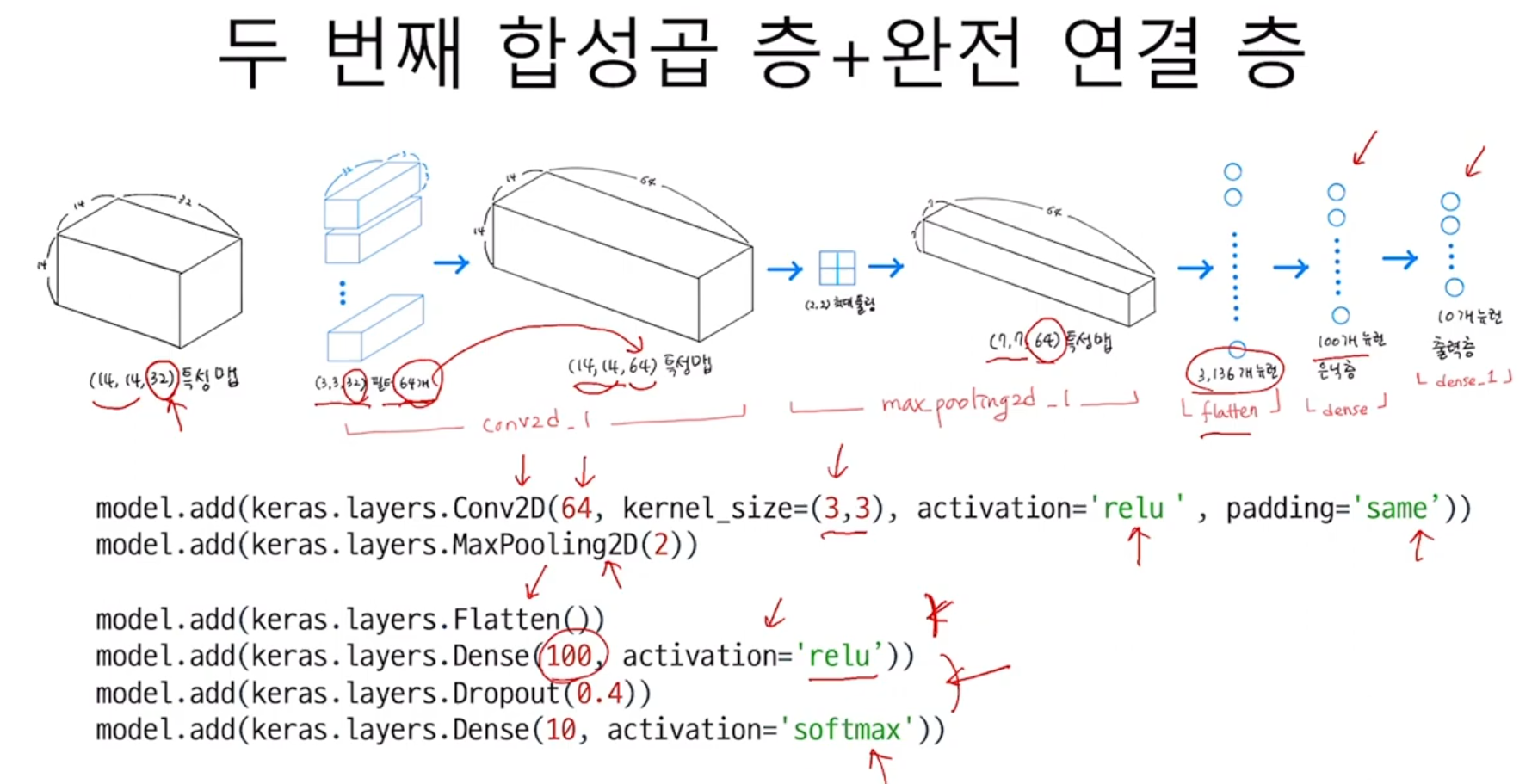

이 합성곱 층은 세임 패딩을 사용한다. 따라서 입력의 가로세로 크기를 줄이지 않는다. 이어지는 풀링 층에서 이 크기를 절반으로 줄인다. 64개의 필터를 사용했으므로 최종적으로 만들어지는 특성 맵의 크기는 (7, 7, 64)가 될 것이다.
이제 이 3차원 특성 맵을 일렬로 펼칠 차례이다. 이렇게 하는 이유는 마지막에 10개의 뉴런을 가진 (밀집) 출력층에서 확률을 계산하기 때문이다. 여기에서는 특성 맵을 일렬로 펼쳐서 바로 출력층에 전달하지 않고 중간에 하나의 밀집 은닉층을 하나 더 두도록 하겠다. 즉 Flatten 클래스 다음에 Dense 은닉층, 마지막으로 Dense 출력층의 순서대로 구성한다.

은닉층과 출력층 사이에 드롭아웃을 넣었다. 드롭아웃 층이 은닉층의 과대적합을 막아 성능을 조금 더 개선해 줄 것이다. 은닉층은 100개의 뉴런을 사용하고 활성화 함수는 합성곱 층과 마찬가지로 렐루 함수를 사용한다. 패션 MNIST 데이터셋은 클래스 10개를 분류하는 다중 분류 문제이므로 마지막 층의 활성화 함수는 소프트맥스를 사용한다.

이제 모델의 구조를 출력해 보겠다.

출력 결과를 보면 합성곱 층과 풀링 층의 효과가 잘 나타나 있다. 첫 번째 합성곱 층을 통과하면서 특성 맵의 깊이는 35가 되고 두 번째 합성곱에서 특성 맵의 크기가 64로 늘어난다. 반면 특성 맵의 가로세로 크기는 첫번째 풀링 층에서 절반으로 줄어들고 두 번째 풀링층에서 다시 절반으로 더 줄어든다. 따라서 최종 특성 맵의 크기는 (7, 7, 64)이다.
모델의 파라미터 개수를 계산해 보자. 첫 번째 합성곱 층은 35개의 필터를 가지고 있고 크기가 (3, 3), 깊이가 1이다. 또 필터마다 하나의 절편이 있다. 따라서 총 3 x 3 x 1 x 32 + 32 = 320개의 파라미터가 있다.
두 번째 합성곱 층은 64개의 필터를 사용하고 있고 크기가 (3, 3), 깊이가 32이다. 역시 필터마다 하나의 절편이 있다. 따라서 총 3 x 3 x 32 x 64 + 64 = 18,496개의 파라미터가 있다.
Flatten 클래스에서 (7, 7, 64) 크기의 특성 맵을 1차원 배열로 펼치면 (3136,) 크기의 배열이 된다. 이를 100개의 뉴런과 완전히 연결해야 하므로 은닉층의 모델 파라미터 개수는 3,136 x 100 + 100 = 313,700개이다. 마찬가지 방식으로 계산하면 마지막 출력층의 모델 파라미터 개수는 1,010개이다.
케라스는 summary() 메서드 외에 층의 구성을 그림으로 표현해 주는 plot_model() 함수를 kderas.utils 패키지에서 제공한다.



네모 상자 안의 내용 중 왼쪽에는 층의 이름이 쓰여 있고 오른쪽에는 클래스가 나타난다. 맨 처음에 나오는 InputLayer 클래스는 케라스가 자동으로 추가해 주는 것으로 입력층의 역할을 한다. 이 입력층은 첫 번째 Conv2D 클래스에 추가한 input_shape 매개변수를 사용한다.
plot_model() 함수의 show_shapes 매개변수를 True로 설정하면 이 그림에 입력과 출력의 크기를 표시해 준다. 또 to_file 매개변수에 파일 이름을 지정하면 출력한 이미지를 파일로 저장한다. dip 개개변수로 해상도를 지정할 수도 있다.


학습을 마치고
다시 공부해 보니 할만하다. 이제 저녁을 먹고 조금 쉬었다가 나머지 두 번째 부분과 8장의 마지막 절도 학습을 진행해 볼 것이다. 그런 다음에는 이제 CNN 수업을 들으며 학습을 이어가 보려고 한다.
'인공지능 > 딥러닝' 카테고리의 다른 글
| 이미지를 위한 인공 신경망 5 - 합성곱 신경망의 시각화 1 : 가중치 시각화 (0) | 2024.10.27 |
|---|---|
| 이미지를 위한 인공 신경망 4 - 합성곱 신경망을 사용한 이미지 분류 2 : 모델 컴파일과 훈련 (0) | 2024.10.27 |
| 이미지를 위한 인공 신경망 2 - 합성곱 신경망의 구성 요소 2 : 케라스 합성곱 층 및 합성곱 신경망의 전체 구조 (1) | 2024.10.27 |
| 이미지를 위한 인공 신경망 1 - 합성곱 신경망의 구성 요소 1 : 합성곱에 대하여 (0) | 2024.10.27 |
| 케라스 11 - tf.data.Dataset 클래스 (0) | 2024.10.26 |





