| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 영어공부
- 정보처리기사실기
- 자바 실습
- SQL
- 데이터분석
- 파이썬
- 중학1-1
- 연습문제
- 컴퓨터구조
- 코딩테스트
- 파이썬라이브러리
- 혼공머신
- 머신러닝
- 정수와유리수
- 데이터입출력구현
- CSS
- JSP/Servlet
- 딥러닝
- pandas
- numpy/pandas
- 자바
- CNN
- html/css
- 데이터베이스
- 컴퓨터비전
- C++
- 중학수학
- 텍스트마이닝
- 정보처리기사필기
- 운영체제
- Today
- Total
클라이언트/ 서버/ 엔지니어 "게임 개발자"를 향한 매일의 공부일지
영상 처리 7 - 연습문제 풀기 2 : 문제 4~5번 본문
점심식사 후에 놀고 싶어서 한참 쉬고 놀고 낮잠을 자다 4시 반에 일어나서 공부를 시작해 본다. 어제 오늘은 공부의 열정이 조금 떨어진 것 같다. 아마도 컴퓨터 비전 공부가 생각만큼 쉽지 않고 지루한 부분이 많아서 하기가 싫은 마음이 큰 것 같다. 그래도 한번 하기로 마음먹은 공부를 포기한 적은 없었으니 다음주 화요일까지는 학습을 진행할 것이다.
오늘 아무리 못해도 4장까지 다 공부하기로 했는데 진도가 많이 늦어졌다. 서둘러서 이제부터 쉬지 않고 공부를 하려고 한다. 지루하다고 영상을 틀어놓고 공부를 했더니 집중은 하나도 되지 않고 영상에만 푹 빠지거나 도리어 잠이 오게 된다. 이제 영상을 완전히 끄고 공부에만 집중할 것이다.
연습문제 풀기 두번째
문제 4번
그림 3-16 b의 원래 영상 f에 다음 필터를 적용한 결과 영상 f'를 제시하시오. 각 필터의 효과에 대해 기술하시오.

이 문제를 풀기 위해서는 그림 3-16 b를 이해해야 한다. 사실 공부할 때는 무슨 말인지 몰라서 그냥 넘어갔다. 이제 확실히 이해해 보기로 하자.

그림 3-16(b)는 2차원 이미지에서 컨볼루션 연산을 적용하는 원리를 설명한다. 이 그림에서 각 위치에 있는 작은 3 × 3 필터(커널)를 원래 영상 f에 적용하여 새로운 값으로 변환하는 과정을 보여준다.
컨볼루션 연산은 필터를 이미지 위에서 슬라이딩하면서, 필터와 이미지의 해당 부분을 곱한 후 합산하여 새로운 값을 계산하는 과정이다. 이때, 각 위치에서의 결과값은 주어진 3 × 3 필터를 해당 위치의 3 × 3 영역에 곱한 후 합산하여 계산된다.
1. 필터와 이미지 매칭
예를 들어, 필터 u가 다음과 같다고 가정한다.

이미지 f의 특정 위치에 대해 해당 위치의 3 × 3 부분과 필터를 곱한 후 합산하여 새로운 값으로 계산된다.
2. 중앙 위치에서의 계산
그림 3-16(b)에서 빨간색으로 표시된 중앙 위치에서 계산을 수행한다고 하자. 원래 이미지 f에서 (2, 2) 위치의 3 × 3 영역을 가져오면 다음과 같다.

이 영역과 필터 u를 곱한 후 합산한다.

합산하면, −1 + 0 + 3 − 1 + 0 + 3 − 1 + 0 + 3 = 6이 된다. 따라서, 결과 이미지 f′의 (2, 2) 위치에는 값 6이 저장된다.
3. 다른 위치로 이동
- 컨볼루션 연산은 이미지 전체를 다루기 위해 이 과정을 다른 위치로 이동하면서 반복한다. 필터가 이미지 위에서 한 픽셀씩 이동하면서 동일한 연산을 수행하여 모든 위치에 대해 결과값을 계산합니다.
4. 패딩
- 그림에서 가장자리 부분의 값들은 보이지 않는 패딩으로 처리할 수 있으며, 주로 값이 0으로 채워진다.
문제 풀기
이제 그림에 대한 이해는 끝났으니 문제로 돌아가서 풀어보기로 하자. 여기까지 이해하는데도 힘들었다.
(1)번 문제
그림 3-16(b)의 원래 영상 f는 다음과 같다.

필터 (1) 적용 결과

필터를 f의 각 위치에 적용하여 결과값을 얻는다. 예를 들어, 필터를 f의 (2, 2) 위치에 적용할 때는 필터와 해당 위치의 3 x 3 부분 행렬을 요소별 곱셈한 후 합산한다.

이와 같은 방식으로 모든 위치를 계산하면 결과 영상 f′는 다음과 같다.

이 필터는 수평 엣지 검출에 사용된다. 상단과 하단의 차이를 강조하여 수평 방향의 경계를 감지한다.
(2)번 문제

필터 (2)는 중심 값을 강조하고 주변 값들을 뺄셈하여 경계를 강화하는 역할을 한다. 이 필터를 원래 영상 f의 각 위치에 적용하여 결과 f′를 계산하면 다음과 같다.

이와 같은 방법으로 모든 위치를 계산하면 결과 영상 f′는 다음과 같이 된다.

이 필터는 라플라시안 필터로, 이미지의 경계를 전체적으로 강조하여 선명하게 만든다. 이 필터는 모든 방향(상하좌우)의 엣지를 감지하는 데 사용된다.
(3)번 문제

필터 (3)은 대각선 방향으로 엣지를 강조하는 역할을 합니다. 이 필터를 f에 적용한 결과는 다음과 같다.

이와 같은 방식으로 계산하면 결과 영상 f′는 다음과 같다.

이 필터는 대각선 엣지 검출에 사용된다. 왼쪽 상단에서 오른쪽 하단으로의 대각선 방향 경계를 강조한다.
문제 5번
예시 3-5에서 나머지 점 3개에 대한 계산 과정을 제시하시오.
문제를 풀기 전에 먼저 예시 3-5부터 이해하기로 하자. 이 부분도 이해하지 못하고 넘어갔던 내용이었다.

이 예시는 동차 좌표와 동차 행렬을 사용해 2D 공간에서 점을 이동 및 회전시키는 과정을 보여준다. 주어진 점 p1=(1, 3)를 이동 및 회전 변환을 통해 새로운 위치로 옮기는 과정이다.

문제 해석 및 설명
1. 동차 좌표로 표현
점 p1=(1, 3)를 동차 좌표로 표현하면

이다. 동차 좌표의 세 번째 요소는 1로 설정하여 2D 좌표를 3D 공간으로 확장한다.
2. 이동 변환 T(2, −1)
이동 행렬 T(2, −1)은 다음과 같이 정의된다.

여기서 x-방향으로 2, y-방향으로 -1만큼 이동하는 변환이다. 앞의 동식에다 대입하면 이 결과가 나온다.
3. 이동 변환을 적용
이동 행렬 T(2,−1)을

에 곱한다.

이 행렬 연산을 하면 위와 같은 결과가 나온다. 결과적으로 p1의 이동 후 위치는 (3, 2)이다.
4. 회전 변환 R(30º)
30도 회전을 위한 회전 행렬 R(30º)은 다음과 같이 정의한다.

이 값은 앞의 공식 cosθ와 sinθ 값을 적용한 결과이다. 이 행렬은 반시계 방향으로 30도 회전시키는 변환이다.
5. 회전 변환을 적용
이동된
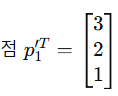
에 회전 행렬을 곱하여 새로운 위치를 얻는다.

최종적으로 회전 후 위치는 (3.598, 0.232)이다. 이제 본 문제를 풀어보겠다.
문제 풀기
우리가 풀어야 할 나머지 세 개의 점은 p2 = (2,4), p3 = (5,1), p4 = (6,3)이다. 각 점 p에 대해 먼저 이동 변환을 적용하고, 이어서 회전 변환을 적용하는 순서로 진행하겠다.
기본 행렬
1. 이동 행렬 T(2,−1)

2. 회전 행렬 R(30∘)

변환 과정
1. p2=(2,4)
1. p2를 동차 좌표로 나타내면

2. 이동 행렬 T를 적용하면

따라서, 이동 후의 좌표는 (4, 3)이다.
3. 회전 행렬 R을 적용하면

회전 후 좌표는 (4.964, 0.098)이다.
2. p3 = (5, 1)
를 동차 좌표로 나타내면

2. 이동 행렬 T를 적용하면

이동 후의 좌표는 (7,0)이다.
3. 회전 행렬 R을 적용하면

회전 후 좌표는 (6.062, −3.5)이다.
3. p4 = (6, 3)
1. p4를 동차 좌표로 나타내면

2. 이동 행렬 T를 적용하면

이동 후의 좌표는 (8, 2)이다.
3. 회전 행렬 R을 적용하면

회전 후 좌표는 (8.228, −1.804)이다.
요약하자면
- p2 = (2, 4) → 이동 후: (4, 3), 회전 후: (4.964, 0.098)
- p3 = (5, 1) → 이동 후: (7, 0), 회전 후: (6.062, −3.5)
- p4 = (6, 3) → 이동 후: (8, 2), 회전 후: (8.228, −1.804)
학습을 마치고
문제가 얼마나 어렵던지 이 두 문제를 푸는데 무려 1시간 반도 넘게 걸렸다. 그래도 문제를 풀면서 공부할 때는 너무 어려워서 그냥 넘어갔던 내용을 다시 학습하면 완전히 이해하고 넘어갈 수 있어서 감사했다.
오늘 안에 4장의 학습은 다 마치지 못할 것 같다. 그래도 중요한 것은 과목을 빠르게 끝마치는 것이 아니라 얼마나 정확하게 잘 이해하고 적용할 수 있느냐이다.
이번 단원은 마치 수학을 공부하는 시간 같았다.
'인공지능 > 컴퓨터 비전' 카테고리의 다른 글
| 영상 처리 9 - 연습문제 풀기 4 : 문제 9~10번 (2) | 2024.11.09 |
|---|---|
| 영상 처리 8 - 연습문제 풀기 3 : 문제 6~8번 (1) | 2024.11.09 |
| 영상 처리 6 - 연습문제 풀기 1 : 문제 1~3번 (0) | 2024.11.09 |
| 영상 처리 5 - 기하 연산과 OpenCV의 시간 효율 (0) | 2024.11.09 |
| 영상 처리 4 - 영역 연산 (2) | 2024.11.09 |





