| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 딥러닝
- 데이터베이스
- 머신러닝
- 중학수학
- 컴퓨터구조
- 운영체제
- 파이썬
- html/css
- 연습문제
- CNN
- 영어공부
- 자바
- 코딩테스트
- numpy/pandas
- 텍스트마이닝
- 데이터입출력구현
- 자바 실습
- C++
- 파이썬라이브러리
- 중학1-1
- SQL
- 정보처리기사실기
- CSS
- 정보처리기사필기
- JSP/Servlet
- pandas
- 정수와유리수
- 컴퓨터비전
- 데이터분석
- 혼공머신
- Today
- Total
클라이언트/ 서버/ 엔지니어 "게임 개발자"를 향한 매일의 공부일지
회귀 알고리즘과 모델 규제 5 - 특성 공학과 규제 1 : 여러 특성을 추가한 다중 회귀 모델과 릿지 회귀와 라쏘 회귀에 대하여 본문
회귀 알고리즘과 모델 규제 5 - 특성 공학과 규제 1 : 여러 특성을 추가한 다중 회귀 모델과 릿지 회귀와 라쏘 회귀에 대하여
huenuri 2024. 9. 28. 23:43이제 3장의 마지막 단원 학습이다. 오늘 낮잠을 많이 잤더니 별로 피곤하지 않아 새벽까지 4장의 학습을 마치고 정처기 실기도 어느 정도 공부할 수 있었으면 좋겠다.
가능할지 모르겠지만 조금씩 다시 회복해 볼 것이다.
지난 시간 복습

음수가 나오는 문제를 해결하기 위해 원래 특성에 제곱한 특성을 추가해주었다.
학습 목표
여러 특성을 사용한 다중 회귀에 대해 배우고, 사이킷런의 여러 도구를 사용해 본다.
복잡한 모델의 과대적합을 막기 위한 릿지와 라쏘 회기를 배운다.
시작하기 전에
혼공머신은 다중 회귀로 농어의 무게를 어느 정도 예측할 수 있지만, 여전히 훈련 세트보다 테스트 세트의 점수가 높은 것이 왠지 찜찜하다. 이 문제를 해결하려면 어떻게 해야 할까?
다중 회귀
여러 개의 특성을 사용한 선형 회귀를 다중 회귀라고 부른다. 선형 회귀 모델이 학습하는 것은 직선이다. 2개의 특성을 사용하는 선형 회귀는 평면을 학습한다.

그럼 특성이 3개일 경우에는 어떨까? 특성이 많은 고차원에서는 선형 회귀가 매우 복잡한 모델을 표현할 수 있다. 이번에는 농어의 길이뿐만 아니라 농어의 높이와 두께도 사용할 것이다. 또한 이전 단원에서처럼 3개의 특성을 가각 제곱하여 추가한다. 그런 다음 각 특성을 서로 곱해서 또 다른 특성을 만든다.
즉 '농어의 길이 X 농어 높이'를 새로운 특성으로 만드는 것이다. 이렇게 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업을 특성 공학이라고 한다.
영어로 다중회귀는 Multiple Regression이라고 하는데 Multinomial Regression이라고 표현하기도 한다. 번역할 때 이를 다항회귀로 번역하기도 하니 둘의 의미는 다중회귀로 모두 같다.
데이터 준비
농어의 특성이 3개로 늘어났기 때문에 데이터를 복사해 붙여 넣는 것도 번거롭다. 판다스는 유명한 데이터 분석 라이브러리이다. 데이터프레임은 판다스의 핵심 데이터 구조이다.
판다스를 사용해 농어 데이터를 인터넷에서 내려받아 데이터프레임에 저장하겠다. 그다음 넘파이 배열로 변환하여 선형 회귀 모델을 훈련한다.
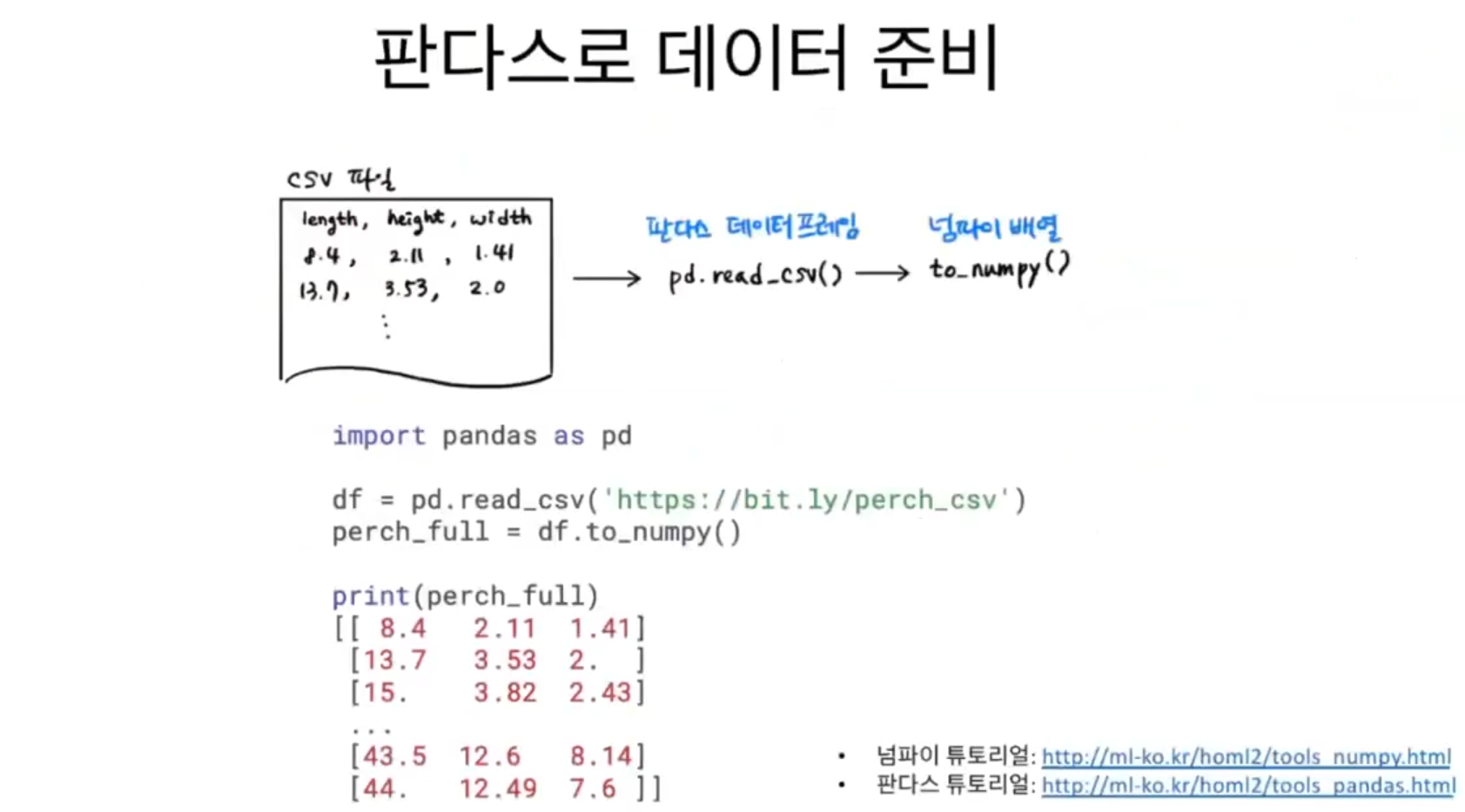
판다스 데이터프레임을 만들기 위해 많이 사용하는 파일은 CSV 파일이다. CSV 파일은 이 그림처럼 콤마로 나 누어져 있는 텍스트 파일이다. 판다스를 읽는 방법은 판다스의 read_csv() 함수에 주소를 넣어주는 것이 전부이다.
타깃 데이터는 이전과 같은 방식으로 준비한다.
사이킷런의 변환기
사이킷런은 특성을 만들거나 전처리하기 위한 다양한 클래스를 제공한다. 사이킷런에서는 이런 클래스를 변환기라고 부른다. 변환기 클래스는 fit(), transform() 메서드를 제공한다.
우리가 사용할 변환기는 PolynomiaFeatures 클래스이다. 이 클래스의 객체를 만든 다음 fit(), transform() 메서드를 차례대로 호출한다.

fit() 메서드는 새롭게 만들 특성 조합을 찾고 transform() 메서드는 실제로 데이터를 변환한다. 변환기는 입력 데이터를 변환하는데 타깃 데이터가 필요하지 않다. 여기서는 2개의 특성(원소)을 가진 샘플 [2, 3]이 6개의 특성을 가진 샘플 [1. 2. 3. 4. 6. 9.]로 바뀌었다.
PolynomiaFeatures 클래스는 기본적으로 각 특성을 제곱한 항을 추가하고 특성끼리 서로 곱한 항을 추가한다. 2와 3을 각각기 제곱한 4와 9가 추가되었고, 2와 3을 곱한 6이 추가되었다. 1은 왜 추가되었을까? 다음 식을 살펴보자.
무게 = a x 길이 + b x 높이 + c x 두께 + d x 1
선형 방정식의 절편은 항상 값이 1인 특성과 곱해지는 계수라고 볼 수 있다. 이렇게 놓고 보면 특성은 (길이, 높이, 두께, 1)이 된다. 하지만 사이킷런의 선형 모델은 자동으로 절편을 추가하므로 굳이 이렇게 특성을 만들 필요가 없다. include_bias=False로 지정하면 된다.
이제 절편을 위한 항이 제거되고 특성의 제곱과 특성끼리 곱한 항만 추가되었다.

이 방식으로 train_input에 적용하여 변환한 데이터를 train_poly에 저장하고 이 배열의 크기를 확인했다. PolynomialFeatures 클래스는 9개의 특성이 어떻게 만들어졌는지 확인하는 아주 좋은 방법을 제공한다. get_feature_names_out() 메서드를 호출하면 9개의 특성이 각각 어떤 입력의 조합으로 만들어졌는지 알려준다.
'x0'은 첫 번째 특성을 의미하고, 'x0^2'는 첫번째 특성의 제곱, 'x0 x1'은 첫 번째 특성과 두 번째 특성의 곱을 나타내는 식이다. 이제 테스트 세트를 변환했다.
다중 회귀 모델 훈련하기
다중 회귀 모델을 훈련하는 것은 선형 회귀 모델을 훈련하는 것과 같다. 다만 여러 개의 특성을 사용하여 선형 회귀를 수행하는 것뿐이다.
먼저 사이킷런의 LinearRegression 클래스를 임포트하고 앞서 만든 train_poly를 사용해 모델을 훈련시킨다. 점수가 아주 높게 나왔다. 농어의 길이뿐 아니라 높이와 두께를 모두 사용했고 각 특성을 제곱하거나 서로 곱해서 다항 특성을 더 추가했다. 이렇게 특성이 늘어나면 선형 회귀의 능력은 매우 강하다는 것을 알 수 있다.
테스트 세트에 대한 점수는 높아지지 않았지만, 농어의 길이만 사용했을 때 있던 과소적합 문제는 더 이상 나타나지 않았다. 특성을 더 많이 추가하면 어떻게 될까?

여기서는 5제곱의 특성까지 만들어 출력했다. 만들어진 특성의 개수가 무려 55개나 된다. 이것은 맞추는 개수보다 특성이 더 많은 값이다. 이 데이터를 사용해 선형 회귀 모델을 다시 훈련했다. 그러자 거의 완벽에 가까운 값이 나옴을 확인했다. 하지만 테스트 세트에 대한 점수는 음수가 나온다. 무슨 일이 일어난 걸까? 특성의 개수를 크게 늘리면 선형 모델은 아주 강력해진다. 훈련 세트에 대해 거의 완벽하게 학습할 수 있지만 이런 모델은 훈련세트에 너무 과대적합된다. 따라서 테스트 세트에서는 형편없는 점수를 만든다.
이 문제를 해결하려면 다시 특성을 줄여야 한다.
규제
규제는 머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 훼방하는 것을 말한다. 선형 회귀 모델의 경우 특성에 곱해지는 계수(또는 기울기) 즉 가중치의 크기를 작게 만드는 일이다. 규제를 정규화라고 부르기도 한다.
앞의 왼쪽 그림은 훈련 세트를 과도하게 학습했고, 오른쪽은 기울기를 줄여 보다 보편적인 패턴을 학습하고 있다.
앞서 55개의 특성으로 훈련한 선형 회귀 모델의 계수를 규제하여 훈련 세트의 점수를 낮추고 대신 테스트 세트의 점수를 높여보겠다. 2장에서 학습했듯이 특성의 스케일이 정규화되지 않으면 여기에 곱해지는 계수 값도 차이 나게 된다. 일반적으로 선형 회귀 모델에 규제를 적용할 때 계수 값이 크기가 서로 많이 다르면 공정하게 제어되지 않을 것이다.
규제를 적용하기 전에 먼저 정규화를 해야 한다. 2장에서는 평균과 표준편차를 직접 구해 특성을 표준점수로 바꾸었다. 이번에는 사이킷런에서 제공하는 StandardScaler 클래스를 사용하겠다.

먼저 StandardScaler 클래스의 객체 ss를 초기화한 후 PolynomialFeatures 클래스로 만든 train_poly를 사용해 이 객체를 훈련한다. 여기서도 훈련 세트로 학습한 변환기를 사용해 테스트 세트까지 변환해야 한다.
선형 회귀 모델에 규제를 추가한 모델을 릿지와 라쏘라고 부른다. 두 모델은 규제를 가하는 방법이 다르다. 릿지는 계수를 제곱한 값을 기준으로, 라쏘는 계수의 절대값을 기준으로 규제를 적용한다. 두 알고리즘 모두 계수의 크기를 줄이지만 라쏘는 아예 0으로 만들 수도 있다.
릿지 회귀
릿지와 라쏘 모두 sklearn.linear_model 패키지 안에 있다. 사이킷런 모델을 사용할 때 편리한 점은 훈련하고 사용하는 방법이 항상 같다는 것이다. 모델 객체를 만들고 fit() 메서드에서 훈련한 다음 score() 메서드로 평가한다.

선형 회귀에서는 거의 완벽에 가까웠던 점수가 조금 낮아졌다. 테스트 세트에 대한 점수도 정상으로 돌아왔다. 확실히 많은 특성을 사용했음에도 불구하고 훈련 세트에 너무 과대적합되지 않아 테스트 세트에서도 좋은 성능을 내고 있다.
릿지와 라쏘 메델을 사용할 때 규제의 양을 임의로 조절할 수 있다. 모델 객체를 만들 때 alpha 매개변수로 규제의 강도를 조절한다. alpha 값이 크면 규제 강도가 세지므로 계수 값을 더 줄이고 조금 더 과소적합 되도록 유도한다. alpha 값이 작으면 계수를 줄이는 역할이 줄어들고 선형 회귀 모델과 유사해지므로 과대적합될 가능성이 크다.
머신러닝 모델에 학습할 수 없고 사람이 알려줘야 하는 파라미터를 하이퍼파라미터라고 부른다. 모델과 관련된 파라미터는 모델 파라미터라고 표현하기도 한다.
적절한 alpha 각을 찾는 한 가지 방법은 alpha 값에 대한 R² 값의 그래프를 그려보는 것이다. 훈련 세트와 테스트 세트의 점수가 가장 가까운 지점이 최적의 alpha 값이 된다.

alpha 값을 0.001에서 100까지 10배씩 늘려가며 릿지 회귀 모델을 훈련한 다음 훈련 세트와 테스트 세트의 점수를 리스트에 저장했다. 그래프는 alpha 값을 0.0004부터 10배씩 늘렸기 때문에 이대로 그래프를 그리면 그래프 왼쪽이 너무 촘촘해진다.
그렇기에 alpha_list에 있는 6개의 값을 동일한 간격으로 나타내기 위해 로그 함수로 바꾸어 지수로 표현했다. 넘파이 로그 함수는 np.log()와 np.log10()이 있다. 전자는 자연 상수 e를 밑으로 하는 자연로그이고, 후자는 10을 밑으로 하는 상용로그이다.
그래프에서 위는 훈련세트, 아래는 테스트 세트이다. 이 그래프 왼쪽을 보면 훈련 세트와 테스트 세트의 점수 차가 아주 크다. 훈련 세트에는 잘 맞고 테스트 세트에는 형편없는 과대적합의 전형적인 모습이다. 반대로 오른쪽은 훈련 세트와 테스트 세트의 점수고 모두 낮아지는 과소적합으로 가는 모습을 보인다.
적절한 alpha 값은 두 그래프가 가장 가깝고 테스트 세트의 점수가 가장 높은 -1, 즉 10의 -1승=0.1이다. alpha 값을 0.1로 하여 최종 모델을 훈련하겠다.
이 모델은 훈련 세트와 테스트 세트 점수가 비슷하게 높고 과대적합과 과소적합 사이에서 균형을 맞추고 있다.
라쏘 회귀
라쏘 모델을 훈련하는 것은 릿지와 매우 비슷하다. Ridge 클래스를 Lasso 클래스로 바꾸는 것이 전부이다.
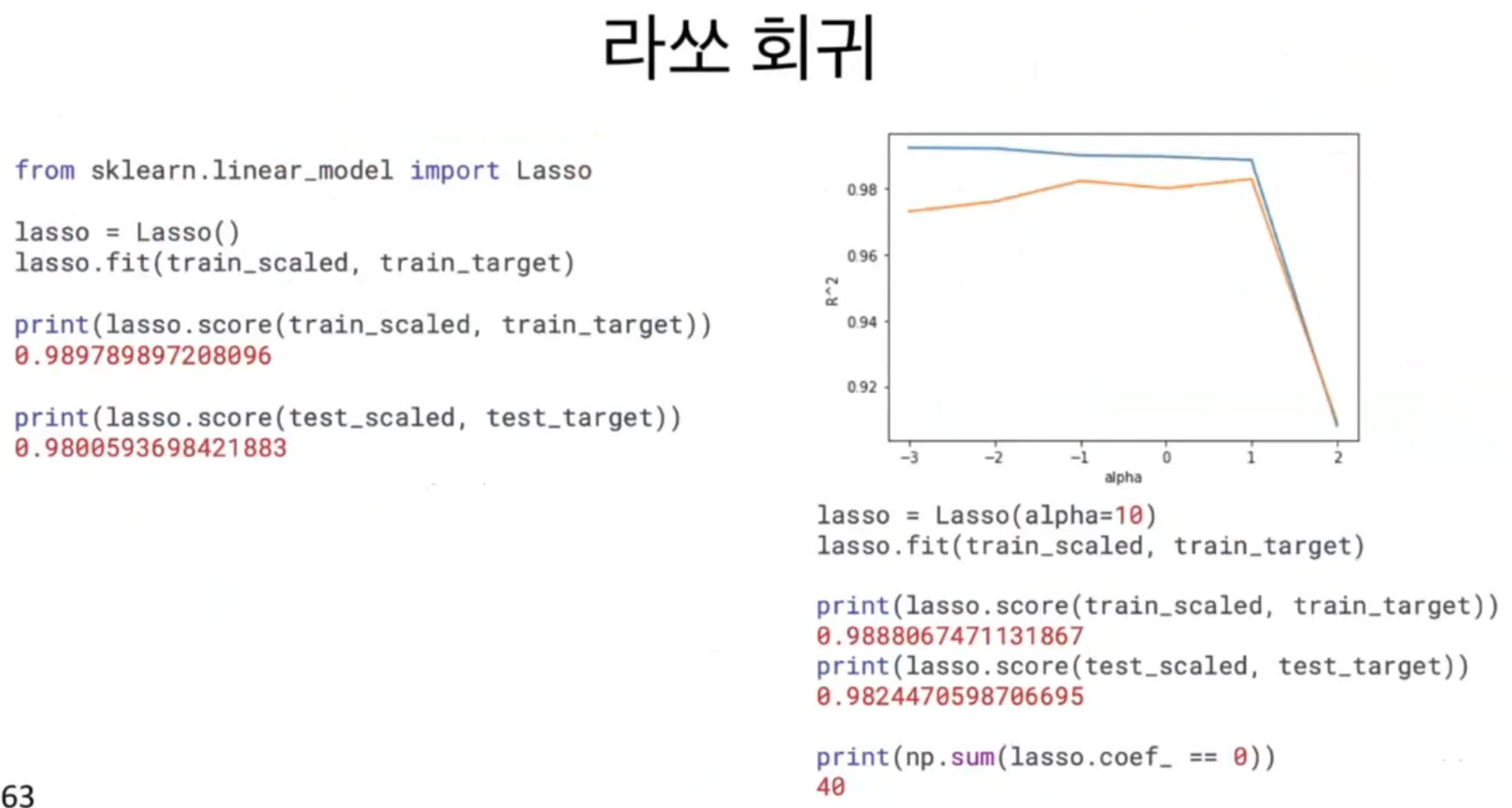
라쏘도 과대적합을 잘 억제한 결과를 보여준다. 테스트 세트의 점수도 릿지만큼 아주 좋다. 이 그래프도 왼쪽은 과대적합을 보여주고 있고, 오른쪽으로 갈수록 훈련 세트와 테스트 세트의 점수가 좁혀지고 있다. 가장 오른쪽은 점수가 크게 떨어진다. 이 지점은 분명 과소적합되는 모델이다.
라쏘 모델에서의 최적의 alpha 값은 10이다. 이 값으로 다시 모델을 훈련하면 과대적합을 잘 억제하고 테스트 세트의 성능도 크게 높임을 볼 수 있다.
55개의 특성을 모델에 주입했지만 라쏘 모델이 사용한 특성은 15개밖에 되지 않는다. 이런 특성 때문에 라쏘 모델을 유용한 특성을 골라내는 용도로 사용할 수 있다.
이제 규제를 적용한 선형 모델을 사용해 농어의 무게를 잘 예측할 수 있게 되었다.
학습을 마치고
이번 수업도 만만치 않은 분량과 어려운 개념들이 가득했다. 그래도 잘 따라왔고 여기까지 온 스스로가 기특하다. 그냥 실행만 시키고 이런 게 있구나 하고 넘어가도 되는데 이처럼 학습일지를 쓰는 이유는 이렇게 공부할 때 제대로 공부가 되기 때문이다.
사람의 기억력은 한계가 있고 자신이 기록하고 힘들고 어렵게 배울수록 머릿속에 남는 법이다. 지금의 어려운 공부도 나중에 다 쓰임새가 있고 필요할 때가 있을 거라 믿는다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| 다양한 분류 알고리즘 1 - 로지스틱 회귀 1 : 로지스틱 회귀 알고리즘으로 클래스 확률 예측하기 (0) | 2024.09.29 |
|---|---|
| 회귀 알고리즘과 모델 규제 6 - 특성 공학과 규제 2 : 스스로 실습하고 문제 풀어보는 시간 (0) | 2024.09.29 |
| 회귀 알고리즘과 모델 규제 4 - 선형 회귀 2 : 스스로 실습하고 문제를 풀어보는 시간 (0) | 2024.09.28 |
| 회귀 알고리즘과 모델 규제 3 - 선형 회귀 1 : 선형회귀와 다중회귀로 농어의 무게 예측해보기 (0) | 2024.09.28 |
| 회귀 알고리즘과 모델 규제 2 - k-최근접 이웃 회귀 2 : 스스로 실습해보고 문제 풀어보기 (0) | 2024.09.28 |





