| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- C++
- 자바 실습
- 운영체제
- JSP/Servlet
- CNN
- 코딩테스트
- 혼공머신
- 텍스트마이닝
- 컴퓨터비전
- 데이터베이스
- 파이썬라이브러리
- SQL
- 정보처리기사필기
- 컴퓨터구조
- pandas
- 정보처리기사실기
- 정수와유리수
- CSS
- 중학수학
- 파이썬
- numpy/pandas
- 중학1-1
- 머신러닝
- 자바
- 데이터분석
- 연습문제
- 데이터입출력구현
- 딥러닝
- 영어공부
- html/css
- Today
- Total
클라이언트/ 서버/ 엔지니어 "게임 개발자"를 향한 매일의 공부일지
텐서플로 3 - 텐서플로 자료 구조 2 : 행렬과 고차원 텐서 본문
이어서 텐서플로 자료 구조에 대해서 학습해본다. 이번에는 행렬에 대해서 학습해보려고 한다.
텐서플로 자료 구조 2
3. 행렬(Matrix)
행렬은 차수가 1인 벡터를 같은 축 방향으로 나열하는 개념이다. 여러 개의 1차원 벡터를 원소로 갖는 1차원 배열이다. 원소의 차수가 1이므로 총 차수는 2가 된다. 텐서플로에서는 '랭크-2' 텐서라고 부른다.
아래의 왼쪽 그림과 같이 랭크-2 텐서에서는 여러 개의 1차원 배열을 원소로 갖는 벡터 형태로 표현된다. 오른쪽 그림은 행과 열이라는 2개의 축을 갖는 2차원 구조로 표현할 수 있다.

다음 예제는 2개의 리스트를 원소로 갖는 리스트를 사용해서 2행 2열 구조의 2차원 행렬 텐서를 만드는 내용이다. CONSTANT 함수에 배열을 입력하면 텐서로 변환해준다.

행 방향과 열 방향으로 2개의 축이 존재하므로 축의 개수를 나타내는 차수는 2개이다. 행의 개수는 2차원 배열을 구성하는 벡터의 개수가 되고, 열의 개수는 각 벡터를 구성하는 원소의 개수가 된다.
stack 함수를 사용해서 행렬을 만들 수 있다.

2차원 구조인 행렬에도 벡터에 적용한 바와 같이 math 모듈의 수학 함수들을 그대로 적용할 수 있다. 같은 위치에 있는 원소들끼리 짝을 이루어 계산한다.
다음 예제는 multiply 함수를 사용하여 각 원소들을 서로 곱하는 과정을 보여준다.


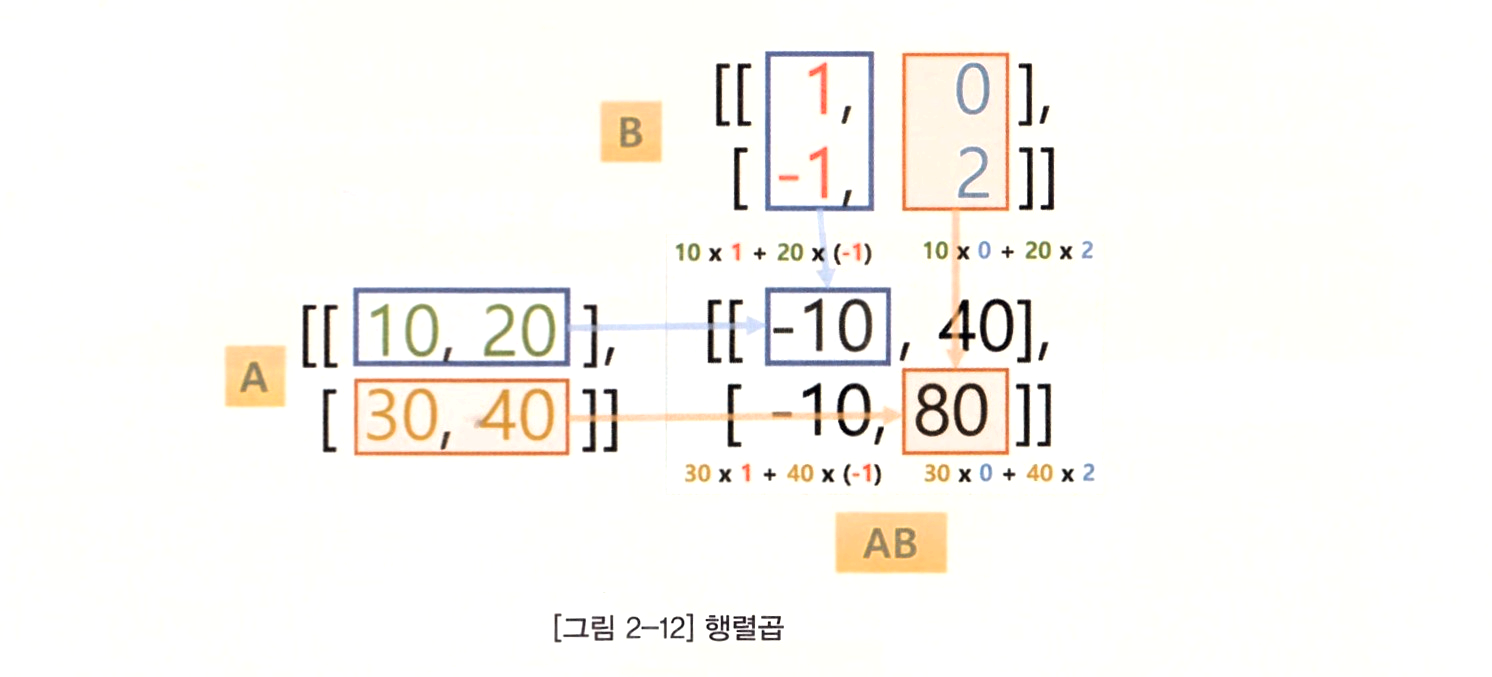
2차원 행렬에 스칼라 값인 3을 곱하면, 행렬의 모든 원소에 3을 곱하게 된다. 선형대수에서 다루는 형렬곱 연산은 matmul 함수를 사용하여 처리한다. 행렬곱은 벡터의 선형결합또는 선형사상 등 선형대수학의 기초가 되는 연산이다.

덧셈 연산은 add 함수로 처리한다. 같은 위치에 있는 원소들끼리 더한 값들은 원래 크기와 같은 행렬에 반환된다. 넘파이 배열을 텐서로 변환할 수 있듯이, 텐서를 넘파이 배열로 변환할 수 있다. numpy() 메소드를 텐서 객체에 적용하면 된다.

4. 고차원 텐서(Tensor)
축이 3개 이상인 고차원 텐서에 대해 알아보자. 먼거 3차원 구조를 갖는 '랭크-3' 텐서 구조를 이해해야 한다. 아래 그림과 같이 랭크-1 텐서를 같은 축 방향으로 결합하면 랭크-2 텐서가 되고, 랭크-2 텐서를 동일한 축 방향으로 결합하면 랭크-3 텐서가 된다. 즉, 1차원 벡터를 나열하면 2차원 행렬이 되고, 2차원 행렬을 나열하면 3차원 텐서가 된다.

다음 예제는 2차원 행렬(행2, 열4)을 먼저 정의하고 각각 mat1, mat2, mat3 변수에 할당한다. 이들 행렬(2차원)을 원소로 갖는 벡터(1차원)을 만들면 랭크-3 텐서가 된다.

stack 함수를 사용하여 3개의 벡터를 결합한다. 위 아래 방향으로 쌓는다고 생각하면 된다.

벡터를 원소라 갖는 행렬을 만드는 방식으로 랭크-3 텐서(1차원 + 2차원 = 3차원)를 정의한다. (행3, 열2) 크기의 행렬을 arr 변수에 정의한 다음, 각 원소에 1개의 축을 갖는 벡터를 입력한다. 즉, 원소 4개가 들어있는 1차원 벡터들로 행렬을 만드는 것이다. constant 함수로 텐서를 변환하면 (3, 2, 4) 크기의 텐서가 된다. 결과적으로 앞에서 만든 텐서와 형태가 동일하다는 것을 알 수 있다.

이번에는 4개의 축을 갖는 4차원 텐서를 만들어보겠다. 앞에서 만든 3차원 텐서 tensor1, tensor2를 stack 함수로 위아래 방향으로 결합해준다. 이처럼 텐서로 변환하면 4개의 축을 갖는 (2, 3, 2, 4) 크기의 랭크-4 텐서가 된다. (3, 2, 4) 크기를 갖는 3차원 배열이 새로운 축 방향으로 2개 결합했기 때문에, 3차원에서 축이 1개 추가되어 4차원 구조가 된다.

학습을 마치고
행렬과 고차원 텐서에 대해서 다루어보았다. 이제 코랩으로 코드를 치는 것도 많이 익숙해졌다. 뭐든 조금 하면 잘할 수 있게 된다. 조금 쉬었다가 다음 단원 학습을 진행해볼 것이다.
텐서플로도 공부해보니 많이 어렵지 않고 할만하다. 그리고 행렬과 수치 연산을 하는 것도 정말 재미있었다.
'인공지능 > 딥러닝' 카테고리의 다른 글
| 딥러닝을 시작합니다 1 - 인공 신경망 1 : 패션 MINIST 데이터셋으로 딥러닝 실습해보기 (0) | 2024.10.04 |
|---|---|
| 텐서플로 4 - 인덱싱과 형태 변환 그리고 자동 미분까지 (0) | 2024.10.04 |
| 텐서플로 2 - 텐서플로 자료 구조 1 : 스칼라와 벡터 (0) | 2024.10.01 |
| 텐서플로 1 - 텐서플로에 대하여 : 텐서플로2와 텐서플로1의 차이점 (0) | 2024.10.01 |
| 딥러닝 개발 환경 구축 - 구글 코랩으로 실행하기 (0) | 2024.10.01 |





