| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- CSS
- 데이터베이스
- 자바스크립트심화
- 자바
- SQL
- JSP
- 컴퓨터비전
- JDBC
- 오블완
- JSP/Servlet
- 머신러닝
- 정보처리기사실기
- 디버깅
- 중학수학
- rnn
- 개발일기
- 연습문제
- 정보처리기사필기
- c언어
- 중학1-1
- 자바 실습
- 자바스크립트
- 데이터분석
- 순환신경망
- 딥러닝
- 상속
- html/css
- 컴퓨터구조
- 파이썬
- 혼공머신
- Today
- Total
클라이언트/ 서버/ 엔지니어 "게임 개발자"를 향한 매일의 공부일지
영상 처리 2 - 이진 영상 본문
이진 영상에 대해서 학습해 보려고 한다. 어제 낮잠을 정말 많이 자서 오늘은 철야를 하며 공부를 하기로 했다.
때로는 컬러 영상이나 명암 영상을 이진 영상으로 변환할 필요가 있다. 이진 영상은 화소가 0 또는 1인 영상이다. 따라서 화소당 1 비트면 정장할 수 있는데, 현재 컴퓨트를 메모리 용량이 크기 때문에 화소당 1바이트를 사용하여 메모리 효율보다 프로그래밍 편려성을 우선하는 경우가 많다. 컴퓨터비전에서는 에지를 검출한 후 에지만 1로 표현하거나 물체를 검출한 후 물체는 1, 배경을 0으로 표시하는 등의 일에 이진 영상을 활용한다.
이진화
명암 영상을 이진화하려면 임계값 T보다 큰 화소는 1, 그렇지 않은 화소는 0으로 바뀌게 된다. 너무 낮게 또는 높게 설정하면 대부분 화소가 물체 또는 배경에 쏠리는 문제가 발생한다. 보통 히스토그램의 계곡 근처를 임계값으로 결정해 쏠림 현상을 누그러뜨린다.

히스토그램은 0, 1, ..., L-1의 명암 단계 각각에 대해 화소의 발생 빈도를 나타내는 1차원 배열이다.


이 예제는 개념을 설명하기 위해 아주 단순한 영상을 사용했다. 실제 영상은 크기도 크고 명암 단계도 256이며 계곡이 분명하지 않을 가능성이 크다.
다음 실습에서는 컬러 영상에서 R 채널을 분리해 명암 영상으로 간주해 히스토그램을 구한다.
실제 영상에서 히스토그램 구하기



이런 게 떴는데 오류는 아니다. 이 메시지는 스파이더(Spyder)에서 플롯이 기본적으로 Plots 창에 표시되지만, 콘솔에도 함께 표시하고 싶다면 "Mute inline plotting" 옵션을 해제해야 한다는 안내이다.
하지만 이 기능은 최신 버전에서 사라졌는지 어떻게 하는지 잘 모르겠다. 어쨌든 별로 중요한 건 아니므로 넘어가기로 했다.

2행은 그래프를 그리기 위해 matplotlib을 불러온다. 5행은 calcHist 함수로 히스토그램을 구한다. 이 함수는 인수를 리스트로 주어야 하는데, 첫 번째와 두 번째 인수는 영상과 영상의 채널 번호다. 채널 번호를 2로 설정했기 때문에 img R 채널에서 히스토그램을 구한다.
세 번째 인수는 히스토그램을 구할 영역을 지정하는 마스크인데, None이므로 전체 영상에서 히스토그램을 구한다. 네 번째 인수 256은 히스토그램의 칸의 수를 지정한다.
실행 결과를 관찰해 보면 큰 계곡이 3개이고 작은 계곡은 아 주 많다. 다음 절의 오츄 알고리즘은 이런 어려움을 피하기 위해 이진화를 최적화 문제로 취급한다.
오츄 알고리즘
오츄는 이진화를 최적화 문제로 바라보았다. 이 식은 모든 명암값에 대해 목적함수 J를 계산하고 J가 최소인 명암값에 대해 목적 함수 J를 계산하고 J가 최소인 명암값을 최적값 t로 정한다. 이렇게 결정한 t을 식 (3.1)의 임계값 T로 사용해 이진화한다.

이진화
다음 프로그램은 오츄 알고리즘으로 이진화를 수행한다.
오츄 알고리즘으로 이진화하기





이렇게 영상이 이진화되어 출력되었다. 6행에서는 threshold 함수의 첫 번째 인수가 img[:, :, 2]이므로 R 채널을 이진화한다. threshold 함수는 알고리즘이 찾은 최적의 임계값과 이진화된 영상을 반환하는데, 6행은 이들을 t와 bin_img 객체에 저장한다.
최적화 문제
컴퓨터 비전은 주어진 문제를 최적화 문제로 공식화해 푸는 경우가 많다.식 (3.2)는 이진화를 최적화 문제로 공식화한 예이다. 매개변수 t는 해 공간을 구성한다. 해 공간이란 발생할 수 있는 모든 해의 집합이다. 모든 해를 다 검사하는 방법을 낱낱 탐색 알고리즘이라 한다.
컴퓨터 비전이 푸는 문제는 해 공간의 크기가 수만~수억 또는 무한대인 경우가 대부분이다. 이런 경우 낱낱 탐색 알고리즘은 시간이 너무 많이 걸려 현실성이 없다. 예를 들어 물체의 외곽선을 찾는 스네이크 알고리즘은 명암 변화와 목선의 매끄러운 정도가 최대가 되는 최적해를 탐욕 알고리즘으로 찾는다. 신경망을 학습할 때는 역전파 알고리즘을 사용해 오류가 최소가 되는 최소해를 빨리 찾는다.
연결 요소
다음 그림은 화소의 연결성을 설명한다. 맨 위쪽은 (j, i)에 위치한 화소의 9개 이 웃 화소를 표시한다. 가운데는 상하좌우에 있는 4개 이웃만 연결된 것으로 간주하는 4-연결성이고 오른쪽은 대각선에 위치한 화소도 연결된 것으로 간주하는 8-연결성이다.
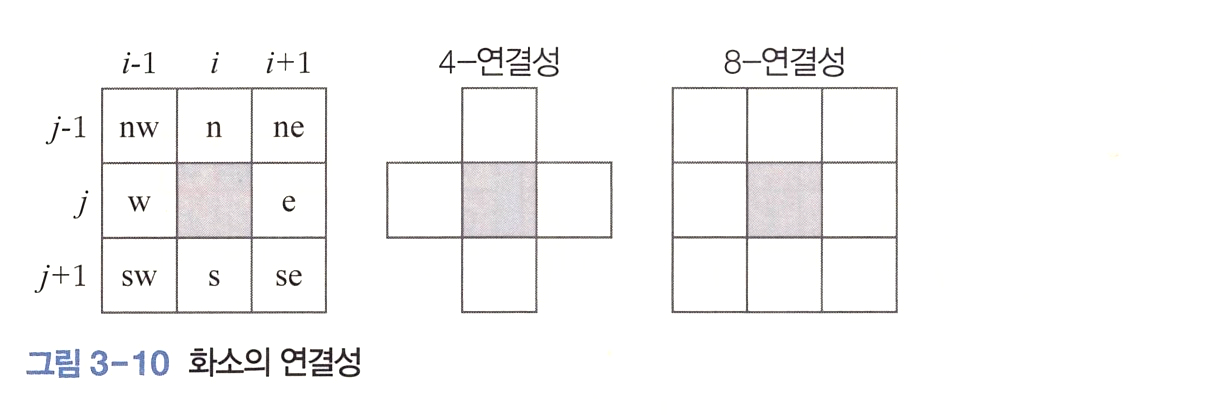
이진 영상에서 1의 각을 가진 연결된 화소의 집합을 연결 요소라 한다. 다음 예시는 4-연결성과 8-연결성에 따라 연결 요소를 표시한 사례다.

모폴로지
영상을 변환하는 과정에서 하나의 물체가 여러 영역으로 분리되거나 다른 물체가 한 영역으로 붙는 경우 등이 발생한다. 이런 부작용을 누그러뜨리기 위해 모폴로지 연산을 사용한다. 이진 영상을 위한 모폴로지와 명암 영상을 위한 모폴로지가 있는데, 여기서는 이진 영상의 모폴로지만 다룬다.
모폴로지는 구주 요소를 이용해 영역의 모양을 조작한다. 아래 그림은 몇 가지 구조 요소의 예이며 이 중에서 회색으로 표시한 것이 중심 화소다.

팽창, 침식 열림, 닫힘
모폴로지의 기본 연산은 팽창과 침식이다. 팽창은 구조 요소의 중심을 1인 화소로 씌운 다음 구조 요소에 해당하는 모든 화소를 1로 바꾼다. 이런 과정을 1인 모든 화소에 적용하면 된다. 침식은 구조 요소의 중심을 1인 화소 p에 씌운 다음 구조 요소에 해당하는 모든 화소가 1인 경우에 p를 1로 유지하고 그렇지 않으면 0으로 바꾼다.

이 예시에서 살펴본 바와 같이 팽창은 작은 홈을 매우거나 끊어진 영역을 하나로 연결하는 등의 효과를 얻을 수 있고 침식은 영역의 경계에 솟은 돌출 부분을 깎는 효과를 얻을 수 있다. 팽창과 침식의 효과는 구조 요소의 모양에 달려 있다.
팽창은 영역을 키우고 침식은 영역을 작게 만든다. 침식을 수행한 영상에 팽창을 적용하면 대략 원래 크기를 유지한다. 침식한 결과에 팽창을 적용하는 연산을 열림이라 하고, 팽창한 결과에 침식을 적용하는 연산을 닫힘이라 한다.
모폴로지 연산
다음 프로그램은 서명을 스캔한 영상에 모폴로지 연산을 적용한다. 5행은 서명 영상을 읽어온다. png 파일에는 4개의 채널이 있으므로 IMREAD_UNCHANGED 인수를 주어 모든 채널을 읽어오도록 지정한다.
모폴로지 효과를 확인할 목적으로 영상의 일부만 잘라 b에 저장하고, 잘라낸 패치를 디스플레이한다.
모폴로지 연산 적용하기







팽창 영상에서는 획이 두꺼워지고 가장자리에 있는 작은 홈이 메워진 것을 확인할 수 있다. 침식 영상은 획이 얇아졌고 심지어 끊어진 곳도 있다. 닫힘 영상은 원래 획의 두께를 대체로 유지한다.
학습을 마치고
이진 영상은 수업 시간에는 그저 실습 위주로 간단히 소개했지만 이처럼 다양하고 복잡한 체계인 줄 몰랐다. 솔직히 수식은 잘 이해가 되지 않지만 지금은 전체를 쭉 훑는다 생각하고 공부하기로 했다.
모폴로지의 팽창, 침식, 열림, 닫힘에 대해서도 기억해두려고 한다.
'인공지능 > 컴퓨터 비전' 카테고리의 다른 글
| 영상 처리 4 - 영역 연산 (0) | 2024.11.09 |
|---|---|
| 영상 처리 3 - 점 연산 (0) | 2024.11.09 |
| 영상 처리 1 - 디지털 영상 기초 (0) | 2024.11.08 |
| 컴퓨터 비전 4 - pafy로 유튜브 영상 연동 및 pytube로 유튜브 영상 다운로드하기 (0) | 2024.11.08 |
| 컴퓨터 비전 3 - 동영상 읽고 출력하는 실습해보기 (0) | 2024.11.08 |





