| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- CNN
- JSP/Servlet
- 파이썬라이브러리
- 중학수학
- 컴퓨터구조
- 데이터입출력구현
- 자바
- 연습문제
- 딥러닝
- 데이터베이스
- 자바 실습
- CSS
- C++
- 운영체제
- 컴퓨터비전
- 코딩테스트
- 중학1-1
- 정보처리기사실기
- 영어공부
- 텍스트마이닝
- 머신러닝
- 데이터분석
- 정수와유리수
- html/css
- numpy/pandas
- 정보처리기사필기
- 혼공머신
- SQL
- 파이썬
- pandas
- Today
- Total
클라이언트/ 서버/ 엔지니어 "게임 개발자"를 향한 매일의 공부일지
에지와 영역 3 - 직선 검출 본문
오늘은 원래 일어나는 시간에 일어나 공부를 시작해 본다. 이제 직선 검출에 대해서 공부해 볼 것이다.
검출한 에지 맵에서 에지 화소는 1, 에지가 아닌 화소는 0으로 표시한다 사람 눈에는 에지가 연결된 선분으로 보이는데, 에지 맵에는 연결 관계가 암시적으로 나타나 있을 뿐 명시적으로 표현되어 있지 않다. 이들을 연결하여 경계선으로 변환하고 경계선을 직선으로 변환하면 이후 단계인 물체 표현이나 인식에 무척 유리하다.
1. 경계선 찾기
8-연결 에지 화소를 서로 연결해 경계선을 구성할 수 있다. 다음 그림은 에지 맵에서 경계선 3개를 찾아 연속된 점의 리스트로 표현하는 사례를 보여준다. OpecCV는 findContours 함수로 이 일을 수행한다.

에지 맵에서 경계선 검출
다음 프로그램은 에지 맵에서 경계선을 검출하고 길이가 임계값 이상인 경계선만 취한다. 16행은 findContours 함수로 경계선을 찾아 contour 객체에 저장한다. 첫 번째 인수는 경계선을 찾을 에지 영상이다. 두 번째 인수는 구멍이 있는 경우 바깥쪽 경계성과 그 안에 있는 구멍의 경계선을 계층적으로 찾는 방식을 지정한다.
이 프로그램은 cv.RETRLIST로 설정해 맨 바깥쪽 경계선만 찾도록 지시한다. 세번째 인수는 경계선을 표현하는 방식을 지정한다.
findContours 함수는 시작점부터 끝점까지 추적한 다음 역추적하여 시작점으로 돌아오도록 경계성을 표현하기 때문에 21행에서 100으로 설정하면 실제로는 길이가 50 이상인 경계선만 남긴다.
에지 맵에서 경계선 찾기



출력한 에지 맵을 보면 잔디밭에서 짧은 잡음 경계선이 많이 발생했다. 길이가 50 이상인 경계선만 골라 원래 영상에 표시한 영상을 보면 잡음 경계선이 거의 사라졌다.
2. 허프 변환
앞 절에서는 이웃한 에지를 연결하여 경계선을 검출한다. 이런 접근 방법은 같은 물체를 구성하는 에지가 자잘하게 끊겨 나타나는 경우 문제가 발생한다. 이런 상황에 허프 변ㅗ한을 적용하면 끊긴 에지를 모아 선분 또는 원 등을 검출할 수 있다.
원리
그림 4-10 a는 두 점을 가지고 허프 변환의 원리를 설명한다. (x, y)를 지나는 직선은 y = ax + b로 표현할 수 있다. a는 기울기고 b는 y축과 만나는 점의 좌표, 즉 y 절편이다. 그림 a에 있는 빨간 점 (x, y) = (1, 3)을 대입하면 b = -a + 3이다. 이 식에서 b와 a를 변수로 간주하면 그림 b의 새로운 공간 (a, b)가 형성된다. 다시 말해 빨간 점 (1, 3)을 지나는 직선은 무수히 많은데 이들 직선은 (a, b) 공간에서 점이 되고 이들 점이 빨간 직선 b = -a + 3을 형성한다.
같은 과정을 파란 점 (3, 1)에 적용하면 그림 b의 (a, b) 공간에서 파란 직선이 된다. (a, b) 공간에서 두 직선이 만나는 점은 (-1, 4)인데 이 점이 그림 a의 원래 공간에서 두 점을 지나는 직선의 기울기와 y 절편이다.

구현
앞에서 설명한 허프 변환은 이상적인 상황을 가정했다. 실제 상황에서 구현하려면 몇 가지 사항을 신중하게 고려해야 한다. 첫째, 그림 4-10에서는 두 점만 고려했는데 현실에서는 많은 점이 있고 점들의 완벽히 일직선을 이루지 못한다. 이 문제는 (a, b) 공간을 이산화하여 해결한다.
둘째, 투표가 이뤄진 누적 배열에 잡음이 많다. 그림 4-11은 가상 누적 배열을 예시한다. 비최대 억제는 잡음이 많은 상태에서 한 점을 결정할 때 컴퓨터 비전이 종종 사용하는 방법이다. 캐니 에지에서는 그림 4-8의 비최대 억제를 사용한 적이 있다. 비최대 억제는 지역 최대가 아닌 점을 억제하고 지역 최대만 남기는 전략이다.

허프 변환 활용
다음 프로그램은 원을 검출하는 허프 변환으로 사과 나무 영상에서 사과를 검출하는 프로그램이다. 17행의 HoughCircles 함수는 첫 번째 인수인 명암 영상에서 원을 검출해 중심과 반지름을 저장한 리스트를 반환한다.
허프 변환을 이용해 사과 검출하기


실행 결과를 분석해보자. 사과를 제대로 찾은 경우도 있지만, 없는 곳을 검출한 거짓 긍정과 있는데 놓친 거짓 부정도 있다. 또한 위치가 틀어진 경우도 있다. HoughCircles 함수의 인수값을 이리저리 변경하며 실험해 보자.
HoughCircles 함수의 인수값 변경하기


인수값을 이리저리 변경해 보았는데 잘 검출이 안 되었다. 맞추기 참 힘든 것 같다. 그래도 여러 실험을 한다는 것 자체가 좋았다.
3. RANSAC
다음 그림은 아웃러이너가 섞여있는 상황을 예시한다. 허프 변환은 어떤 선분이 있는지 모르게 때문에 모든 점에 같은 투표 기회를 준다. 누적 배열에 잡음이 많이 발생하는 원인이다. 허프 변환은 비최대 억제를 이용해 문제 해결을 시도하지만 그림 4-12 상황에서 빨간 직선 2개를 출력할 가능성이 높다.
최소평균제곱오차(LMSE) 알고리즘은 모든 점을 대상으로 오류를 계산하고 최소 오류를 범하는 직선을 찾는다. 이 그림에서 최소평균제곱오차로 추정한 파란 직선을 보여주는데 아웃라이어의 영향으로 실제에서 벗어난 직선을 찾는다. 이 알고리즘은 인라이어와 아웃라이어 구별 없이 모든 샘플이 동등한 자격으로 오류 계산에 참여하기 때문에 아웃라이어의 영향을 크게 받을 수밖에 없다. 허프 변환과 최소평균제곱오차는 둘 다 아웃라이어에 민감한 강인하지 않은 기법이다.

아웃라이어를 걸러내는 과정알 가진 추정 기법을 강인한 추정이라 부른다. 예를 들어 같은 물건의 길이를 5번 측정했는데 [16, 1, 1, 1, 1]을 얻었다면 16은 아웃라이어일 가능성이 매우 높다. 평균으로 길이를 추정하면 4가 되는데 평균은 아웃라이어에 대처하는 능력이 전혀 없다고 말할 수 있다.

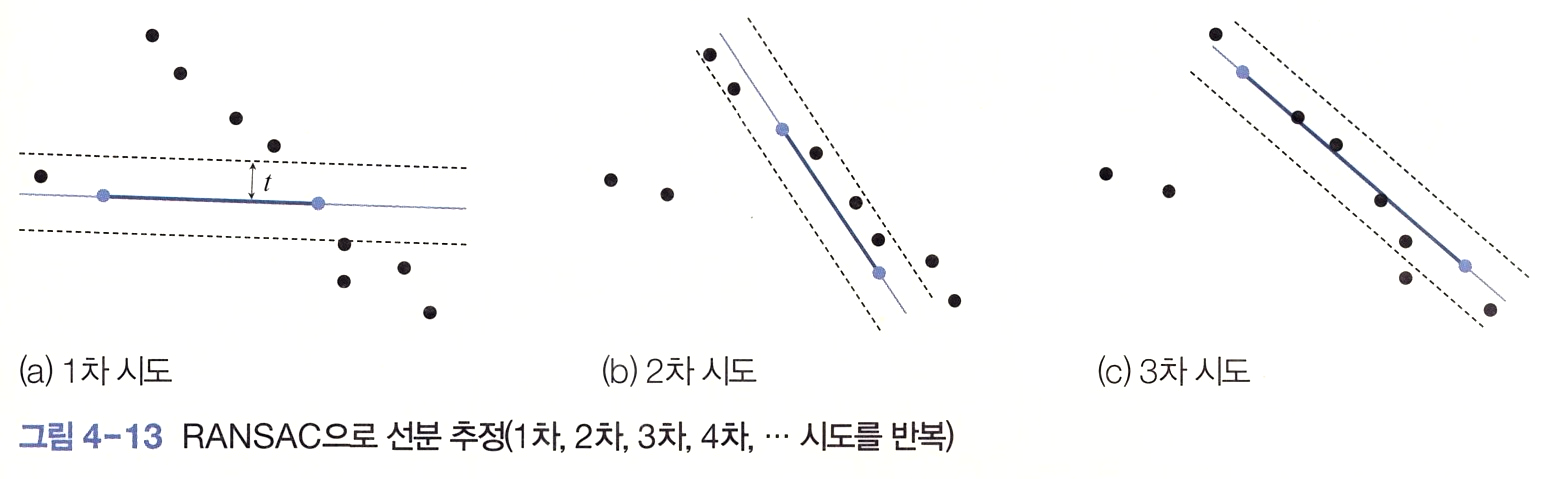
RANSAC은 반복 횟수가 많을수록 진짜 직선을 찾을 가능성이 높아진다. 반면 시간은 더 걸리기 때문에 적절한 값을 설정해야 한다 RANSAC은 난수를 사용하기 때문에 실행할 때마다 다른 결과를 출력한다.
학습을 마치고
허프 변환으로 사과를 검출하고 에지 맵에서 경계선을 찾아보는 실습을 진행해 보았다. 그래프를 해석하는 부분은 아직 이해가 잘 되지 않는 부분이 많지만 연습문제를 풀며 이해하는 부분이 많으리라 생각하며 넘어가기로 했다.
머신러닝할 때 공부했던 최소평균오차 알고리즘도 등장하고 있다.
'인공지능 > 컴퓨터 비전' 카테고리의 다른 글
| 에지와 영역 6 - 대화식 분할 (0) | 2024.11.10 |
|---|---|
| 에지와 영역 4 - 영역 분할 1 : 배경이 단순한 영역의 영역 분할과 슈퍼 화소 분할 (0) | 2024.11.10 |
| 에지와 영역 2 - 캐니 에지 (0) | 2024.11.09 |
| 에지와 영역 1 - 에지 검출 (0) | 2024.11.09 |
| 영상 처리 9 - 연습문제 풀기 4 : 문제 9~10번 (2) | 2024.11.09 |





