| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- CNN
- C++
- 자바
- 코딩테스트
- 연습문제
- 머신러닝
- html/css
- 딥러닝
- SQL
- 중학1-1
- 혼공머신
- CSS
- 텍스트마이닝
- 중학수학
- 파이썬
- 정보처리기사필기
- 운영체제
- 컴퓨터구조
- 데이터입출력구현
- 데이터분석
- 정수와유리수
- numpy/pandas
- 정보처리기사실기
- JSP/Servlet
- 파이썬라이브러리
- 컴퓨터비전
- 자바 실습
- 데이터베이스
- 영어공부
- pandas
- Today
- Total
클라이언트/ 서버/ 엔지니어 "게임 개발자"를 향한 매일의 공부일지
다양한 분류 알고리즘 3 - 확률적 경사 하강법 1 : 확률적 경사 하강법과 손실 함수에 대하여 본문
이제 확률적 경사 하강법에 대해서 공부해보려고 한다. 이 내용에 대한 강의도 1시간이 넘는 무척 많은 분량이다. 책도 함께 학습하며 또다시 새로운 전진을 해볼 것이다.
학습 목표
경사 하강법 알고리즘을 이해하고 대량의 데이터에서 분류 모델을 훈련하는 방법 배우기
시작하기 전에
한빛마켓은 럭키백 이벤트를 오픈하고 나서 매출이 껑충 뛰었다. 영업팀은 매주 7개의 생선 중에서 일부를 무작위로 골라 머신러닝 모델을 학습할 수 있게 훈련 데이터를 제공하고 있다. 하지만 수산물을 공급하겠다는 곳이 너무 많아 샘플을 골라내는 일이 너무 힘들다. 게다가 추가되는 수산물은 아직 샘플을 가지고 있지 않다.
영업팀은 새로운 생선이 도착하는 대로 가능한 즉시 훈련 데이터를 제공하겠다고 약속했다. 하지만 어느 생선이 먼저 올지, 모든 생선이 도착할 때까지 기다릴 수 없다. 이제 어떻게 해야 할까?

점진적인 학습
한빛 마켓이 당면한 문제는 훈련 데이터가 한 번에 준비되는 것이 아니라 조금씩 전달되다는 것이다. 그렇다면 기존의 훈련 데이터에 새로운 데이터를 추가하여 모델을 매 일매일 다시 훈련하면 어떨까? 이렇게 하면 매일 추가되는 새로운 데이터를 활용해 모델을 훈련할 수 있다. 한 가지 단점은 시간이 지날수록 데이터가 늘어나는 것이다.
또 다른 방법은 새로운 데이터를 추가할 때 이전 데이터를 버림으로써 훈련 데이터 크기를 일정하게 유지하는 것이다. 이렇게 하면 데이터셋의 크기가 너무 커지지 않을 수 있다. 하지만 데이터를 버릴 때 다른 데이터에 없는 중요한 생선 데이터가 포함되어 있다면 큰일이다.
앞서 훈련한 모델을 버리지 않고 새로운 데이터에 대해서만 조금씩 더 훈련할 수 없을까? 그렇게 된다면 훈련에 사용한 데이터를 모두 유지할 필요도 없고 앞서 학습한 생선을 까먹을 일도 없을 것이다. 이런 식의 훈련을 점진적 학습 또는 온라인 학습이라고 부른다.
대표적인 점진적 학습 알고리즘은 확률적 경사 하강법이다.
확률적 경사 하강법
확률적이라는 말은 '무작위하게' 혹은 '랜덤하게'의 기술적인 표현이다. 경사는 기울기를 말하는 것이고, 하강법은 내려가는 방법이다. 다시 말해 경사 하강법은 경사를 따라 내려가는 방법이다. 가장 빠른 길은 경사가 가장 가파른 길이다.
가장 가파른 경사를 따라 원하는 지점에 도달하는 것이 목표이다. 긴 다리를 생각해 보자. 만약 한 번에 걸음이 너무 크면 경사를 따라 내려가지 못하고 오히려 올라갈 수 있다.
실제로 산에서 내려올 때는 천천히 조금씩 내려와야 한다 경사 하강법도 마찬가지이다. 가장 가파른 길을 찾아 내려오지만 조금씩 내려오는 것이 중요하다.

경사 하강법으로 내려올 때 가장 가파른 길을 찾는 방법은 무엇일까? 훈련 세트를 사용해 모델을 훈련하기 때문에 경사 하강법도 당연히 훈련 세트를 사용하여 가장 가파른 길을 찾을 것이다. 그런데 전체 샘플을 사용하지 않고 딱 하나의 샘플을 훈련 세트에서 랜덤하고 골라 가장 가파른 길을 찾는다. 이처럼 훈련 세트에서 랜덤하게 하나의 샘플을 고르는 것이 확률적 경사 하강법이다.
확률적 경사 하강법은 훈련 세트에서 랜덤하게 하나의 샘플을 선택하여 가파른 경사를 조금 내려간다. 그다음 훈련 세트에서 랜덤하게 또 다른 샘플을 하나 선택하여 경사를 조금 내려간다. 이런 식으로 전체 샘플을 모두 사용할 때까지 계속한다. 모든 샘플을 다 사용하면 다시 처음부터 시작한다. 이렇게 만족할만한 위치에 도달할 때까지 계속 내려간다.
확률저 경사 하강법에서 훈련 세트를 한 번 모두 사용하는 과정을 에포크라고 부른다. 일반적으로 경사 하강법은 수십, 수백 번 이상 에포크를 수행한다. 여러 개의 샘플을 이용해 경사하강법을 수항하는 방식을 미니 배치 경사 하강법이라고 한다. 극단적으로 한 번 경사로를 따라 이 동하기 위해 전체 샘플을 사용하는 것을 배치 경사 하강법이라고 부른다. 전체 데이터를 사용하기 때문에 가장 안정적인 방법이 될 수 있다. 하지만 전체 데이터를 사용하면 그만큼 컴퓨터 자원을 많이 사용하게 된다. 어떤 경우는 데이터가 너무 많아 한 번에 전체 데이터를 모두 읽을 수 없게 된다.
확률적 경사 하강법은 훈련 세트를 사용해 산 아래에 입는 최적의 장소로 조금씩 이동하는 알고리즘이다. 이 때문에 훈련 데이터가 모두 준비되어 있지 많고 매일매일 업데이트되어도 학습을 계속 이어갈 수 있다.
확률적 경사 하강법을 꼭 사용하는 알고리즘은 신경망 알고리즘이다. 신경망은 일반적으로 많은 데이터를 사용하기 때문에 한번에 모든 데이터를 사용하기 어렵다.
하지만 어디서 내려가야 할까?
손실 함수
손실 함수는 어떤 문제에서 머신러닝 알고리즘이 얼마나 엉터리인지 측정하는 기준이다. 손실 함수의 값은 작을수록 좋다. 하지만 어떤 값이 최소값인지는 알지 못한다. 가능한 많이 찾아보고 만족할만한 수준이라면 산을 다 내려왔다고 인정해야 한다. 이 값을 찾아서 조금씩 이동하려면 확률적 경사 하강법이 잘 맞을 것이다.
비용 함수(cost function)는 손실 함수의 다른 말이다. 손실 함수는 샘플 하나에 대한 손실을 정의하고, 비용 함수는 훈련 세트에 있는 모든 샘플에 대한 손실 함수의 합을 말한다. 하지만 보통 이 둘을 엄격히 구분하지 않고 섞어서 사용한다.

분류에서 손실은 아주 확실하다. 이 예시에서 정확도는 0.5이다. 하지만 정확도에는 치명적인 단점이 있다. 앞의 그림과 같이 4개의 샘플만 있다면 가능한 정확도는 0, 0.25, 0.5, 0.75, 1 이렇게 5가지뿐이다. 정확도가 이렇게 듬성듬성하다면 경사 하강법을 이용해 조금씩 움직일 수 없다. 산의 경사면은 확실히 연속적이어야 한다.
기술적으로 말하면 손실 함 수는 미분 가능해야 한다. 그럼 어떻게 연속적인 손실 함수를 만들 수 있을까? 로지스틱 회귀 모델은 확률을 출력할 수 있는데, 예측은 0 또는 1이지만 확률은 0~1 사이의 어떤 값도 될 수 있다.
로지스틱 손실 함수
첫 번째 샘플의 예측은 0.9이므로 양성 클래스의 타깃인 1과 곱한 다음 음수로 바꿀 수 있다. 예측이 1에 가까울수록 좋은 모델이다. 1에 가까울수록 예측과 타켓의 곱의 음수는 점점 작아진다.
두 번째 샘플의 예측은 0.3이다. 세 번째 샘플의 타깃은 음성 클래스라 0이다. 이 값을 예측 확률인 0.2와 그대로 곱해서는 곤란하다. 무조건 0이 되기 때문이다. 대신 예측값도 양성 클래스에 대한 예측으로 바꾼다. 즉 1 - 0.2 = 0.8로 사용한다.
네 번째 샘플의 손실이 높다. 여기에서 예측 확률에 로그 함수를 적용하면 더 좋다. 예측 확률의 범위는 0~1 사이인데 로그 함수는 이 사이에서 음수가 되므로 최종 손실 값은 양수가 된다. 또 로그 함수는 0에 가까울수록 아주 큰 음수가 되기 때문에 손실을 아주 크게 만들어 모델에 큰 영향을 미칠 수 있다.
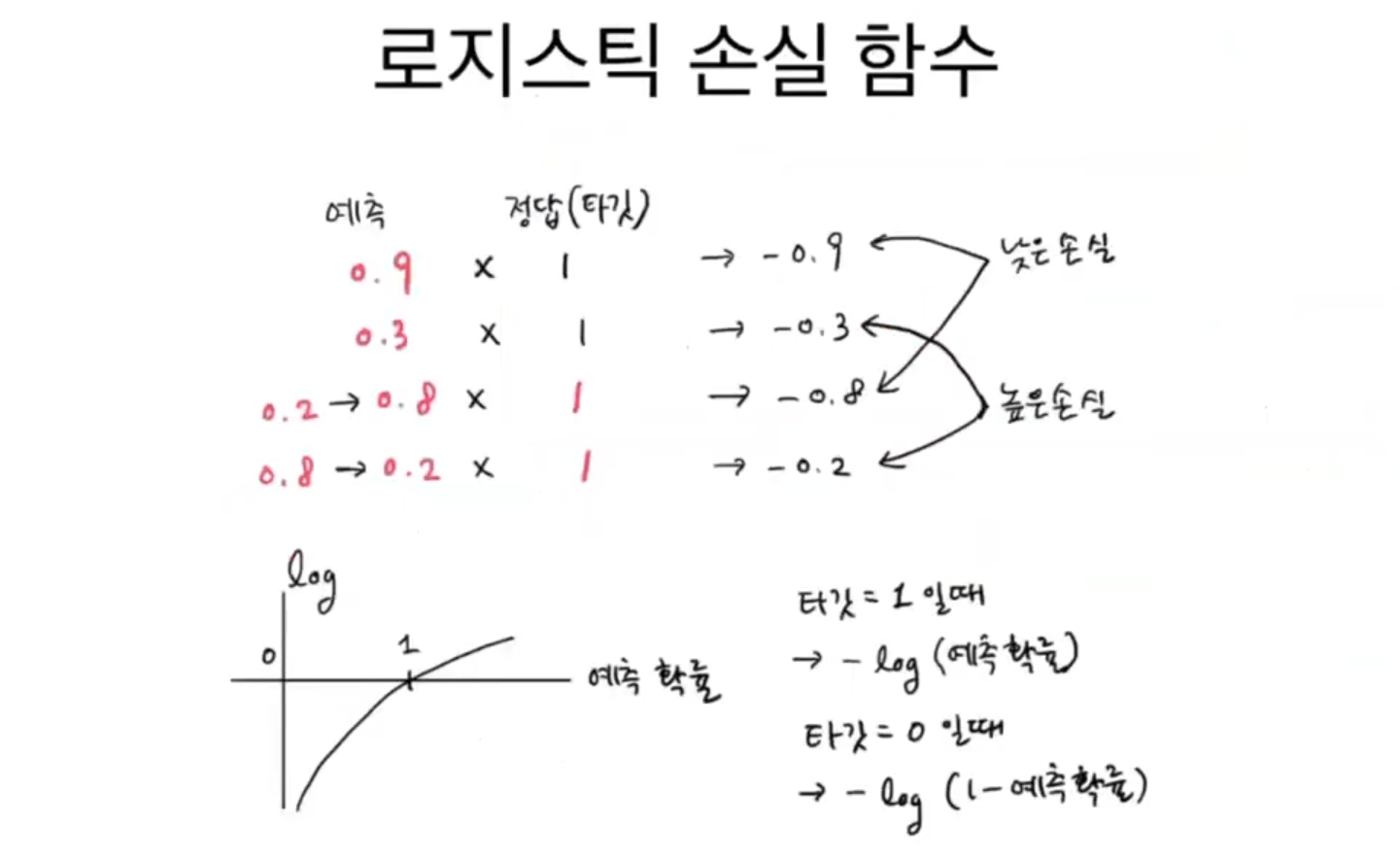
양성 클래스(타깃 = 1)일 때 손실은 -log(예측 확률)로 계산한다. 확률이 1에서 멀어져 0에 가까워질수록 손실은 아주 큰 양수가 된다. 음성 클래스(타깃 = 0)일 때 손실은 -log(1-예측 확률)로 계산한다. 이 예측 확률이 0에서 멀어져 1에 가까워질수록 손실은 아주 큰 양수가 된다.
이 손실 함수를 로지스틱 손실 함수라고 부른다. 또는 이진 크로스엔트로피 손실 함수라고도 부른다. 다중 분류에서 사용하는 손실 함수를 크로스엔트로피 손실 함수라고 부른다. 회귀에서 손실 함수로 평균 절대값 오차를 사용할 수 있다. 타깃에서 예측을 뺀 절대값을 모든 샘플에 평균한 값이다. 또는 평균 제곱 오차를 많이 사용한다. 타깃에서 예측을 빤 값을 제곱한 다음 모든 샘플에 평균한 값이다. 이 값이 작을수록 좋은 모델이다.
손실 함수를 직접 계산하는 일은 드물다. 하지만 손실 함수가 무엇인지, 왜 정의를 해야 하는지 이해하는 것이 중요하다. 이제 확률적 경사 하강법을 사용한 분류 모델을 만들어보겠다.
SGDClassifier
판타스 데이터 프레임을 만들어본다. 그 다음 Species 열을 제외한 나머지 5개는 입력 데이터로 사용한다. Species 열은 타깃 데이터이다. 사이킷런의 train_test_split() 함수를 이용해 이 데이터를 훈련 세트와 테스트 세트로 나누었다. 이 둘을 표준화 전처리하고 특성값의 스케일에 맞춘 두 넘파이 배열을 준비한다. 여기까지는 이전에 배운 것과 같다.
확률적 경사 하강법을 제공하는 SGDClassifier 클래스를 임포트한다.

SGDClassifier의 객체를 만들 때 2개의 매개변수를 지정한다. loss는 손실 함수의 종류를 지정한다. 여기서는 loss='log_loss'로 지정하여 로지스틱 손실 함수를 지정했다. max_iter는 수행할 에포크 횟수를 지정한다. 10으로 지정하여 전체 훈련 세트를 10회 반복했다.

출력된 훈련 세트와 테스트 세트의 정확도가 낮다. 아마도 지정한 반복 횟수 10번이 부족한 것으로 보인다. 확률적 경사 하강법은 점진적 학습이 가능하다. SGDClassifier 객체를 다시 만들지 않고 훈련한 모델 sc를 추가로 더 훈련해 보겠다. 모델을 이어서 훈련할 때는 partial_fit() 메서드를 사용한다. 이 메서드는 fit() 메서드와 같지만 호출할 때마다 1 에포크씩 이어서 훈련할 수 있다.
점수를 확인해 보면 정확도가 향상되었다. 하지만 얼마나 더 훈련해야 할까?
에포크와 과대/과소적합
확률적 경사 하강법을 사용한 모델은 에포크 횟수에 따라 과소적합이나 과대적합이 될 수 있다. 왜 이런 현상이 일어날까? 에포크 횟수가 적으면 모델이 훈련 세트를 덜 학습한다. 마치 산을 다 내려오지 못하고 훈련을 마치는 셈이다. 에포크 횟수가 충분히 많으면 훈련 세트를 완전히 학습할 것이다. 훈련 세트에 아주 잘 맞는 모델이 만들어진다.
바꾸어 말하면 적은 에포크 횟수 동안에 훈련한 모델은 훈련 세트와 테스트 세트에 잘 맞지 않는 과소적합될 모델일 가능성이 높다.
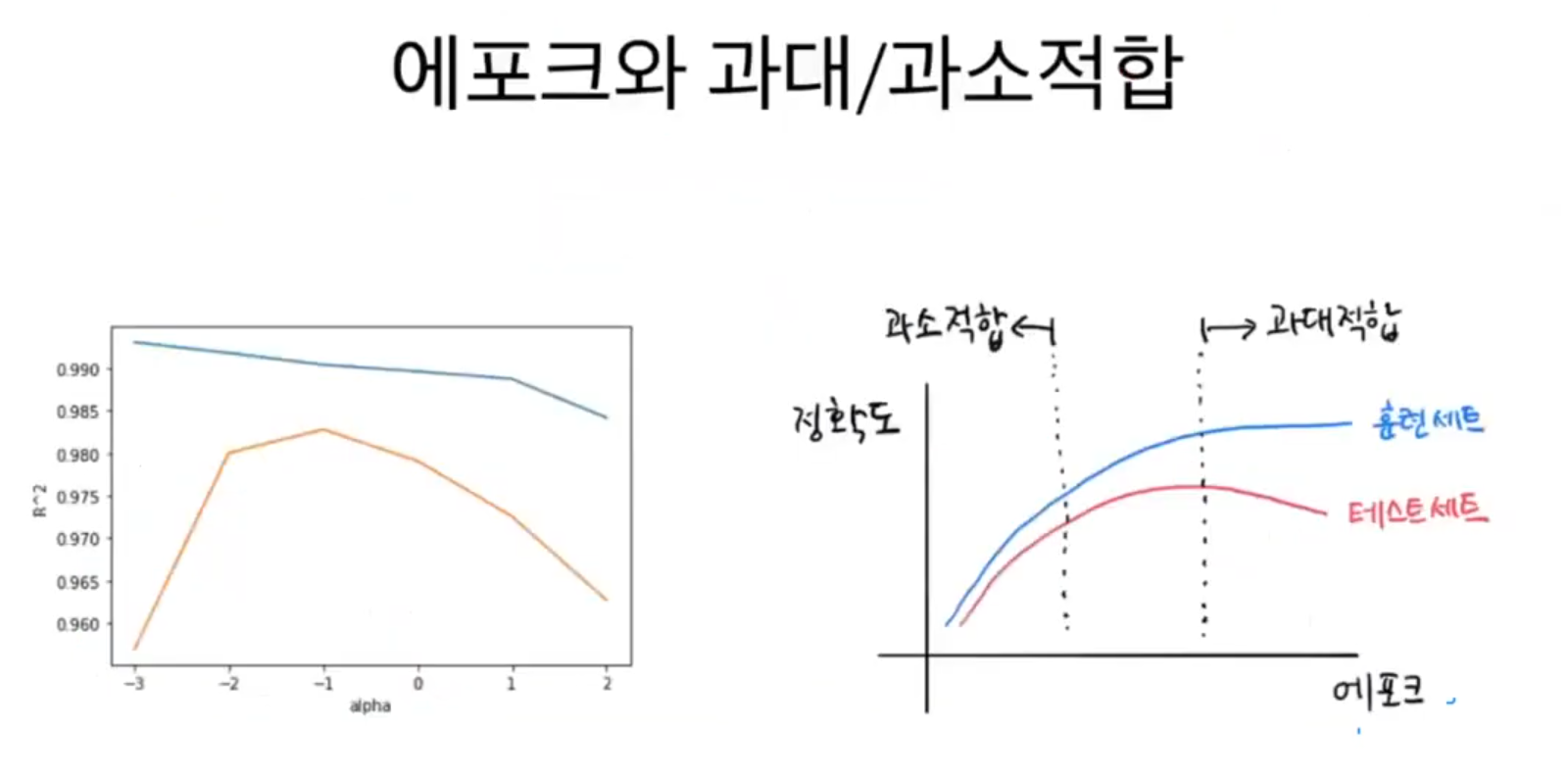
이 그래프는 에포크가 진행됨에 따라 모델의 정확도를 나타낸 것이다. 훈련 세트 점수는 에포크가 진행될수록 꾸준히 증가하지만 테스트 세트의 점수는 어느 순간 감소하기 시작한다. 바로 이 지점이 모델이 과대적합되기 시작하는 곳이다. 과대 적합이 시작하기 전에 훈련을 멈추는 것을 조기 종료라고 한다.
이제 준비한 데이터셋으로 그래프를 만들어보겠다. 이 예제에서는 fit() 메서드를 사용하지 않고 partial_fit() 메서드만 사용한다. 이 메서드만 사 용하려면 훈련 세트에 있는 전체 클래스의 레이블을 partial_fit() 메서드에 전달해 주어야 한다. 이를 위해 np.unique() 함수로 train_target에 있는 7개 생선의 목록을 만든다. 또 에포크마다 훈련 세트와 테스트 세트에 대한 점수를 기록하기 위해 2개의 리스트를 준비한다.

300번의 에포크 동안 훈련을 반복하여 진행해보겠다. 데이터가 작기 때문에 아주 잘 드러나지는 않지만, 100번째 에포크 이후에는 훈련 세트와 테스트 세트의 점수가 조금씩 벌어지고 있다. 또 확실히 에포크 초기에는 과소적합되어 훈련 세트와 테스트 세트의 점수가 낮다.
SGDClassifier의 반복 횟수를 100에 맞추고 모델을 다시 훈련해 보겠다. 그리고 최종적으로 훈련 세트와 테스트 세트에서 점수를 출력한다.
SGDClassifier는 일정 에포크 동안 성능이 향상되지 않으면 더 훈련하지 않고 자동으로 멈춘다. tol 매개변수에서 향상될 최소값을 지정한다. 최종 점수가 좋다. 확률적 경사 하강법을 사용한 생선 분류 문제도 성공적으로 수행했다.
SGDClassifier의 loss 매개변수를 잠시 알아보겠다. 한지 손실은 서포트 벡터 머신이라 불리는 또 다른 머신러닝 알고리즘을 위한 손실 함수이다. SGDClassifier가 여러 종류의 손실 함수를 loss 매개변수에 지정하여 다양한 머신러닝 알고리즘을 지원한다.
학습을 마치고
이번 단원도 무척 어려운 개념을 다루고 있었지만 그래도 끝까지 공부를 마쳐보았다. 한 단원을 학습하는데 보통 1시간 반 정도 걸린다. 중간에 너무 졸려서 10분 정도 낮잠을 자기도 했다.
이제 머신러닝 단원은 두 단원 정도 남아있다. 빨리 머신러닝을 마치고 딥러닝으로 넘어가고 싶지만 기본이 있어야 딥러닝도 제대로 이해할 수 있을 것 같다. 5단원 학습까지는 마치고 정보처리기사 실기 공부를 오늘은 꼭 해야 할 것 같다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| 트리 알고리즘 1 - 결정 트리 1 : 결정 트리 알고리즘으로 레드 와인과 화이트 와인 분류하기 (0) | 2024.09.29 |
|---|---|
| 다양한 분류 알고리즘 4 - 확률적 경사 하강법 2 : 스스로 실습하고 문제 풀어보는 시간 (0) | 2024.09.29 |
| 다양한 분류 알고리즘 2 - 로지스틱 회귀 2 : 스스로 실습하고 문제 풀어보는 시간 (0) | 2024.09.29 |
| 다양한 분류 알고리즘 1 - 로지스틱 회귀 1 : 로지스틱 회귀 알고리즘으로 클래스 확률 예측하기 (0) | 2024.09.29 |
| 회귀 알고리즘과 모델 규제 6 - 특성 공학과 규제 2 : 스스로 실습하고 문제 풀어보는 시간 (0) | 2024.09.29 |





